各种排序算法详解.
http://blog.csdn.net/hguisu/article/details/7776068
快速排序, 快速搞定: 挖坑填数法:
http://blog.csdn.net/morewindows/article/details/6684558
快排时间复杂度退化到 O(n2) 的问题
http://blog.chys.info/2012/02/quicksort/
各种排序的时间复杂度:
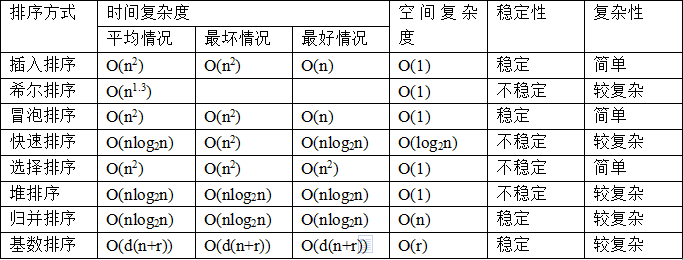 快速排序, 归并排序, 堆排序比较:
快速排序, 归并排序, 堆排序比较:
* 全内存的话,大数据快排平均速度比归并和堆排序快,复杂度相同但是消耗更小. 不稳定. 但通过改进是算法后, 可以变的稳定. 变稳定后, 仍然是最快速的排序算法. (元素大小相同的时候, 比较原始索引值, 就没有相等的元素了.)
* 归并在外部排序,比如磁盘文件的情况下比快排好,因为快排很依赖数据的随机存取,而归并是顺序存取,对磁盘这种外存比较友好. 稳定.
* 堆排序常数项比较高,速度最慢. 能想到的地方是在快速排序t递归过深,感觉退化比较厉害时候会用堆排(堆排序完全不用递归, 空间复杂度最小. O(1) ). 不稳定.
//* 快速排序. 挖坑法.
//* 快速排序的基本思想是左右分治. 选取一个基准元素. 比较,移动, 让左侧的所有元素都小于等于基准元素. 右侧的所有元素都大于等于基准元素.
// 这样基准元素自己就已经找到了自己的位置了. 然后分别对左侧和右侧再进行快速排序.
//* 快速排序之所以快是因为每次找到一个元素的位置后, 再寻找左侧数组和右侧数组的下个元素的位置的时候, 只需要在这个子数组中查找, 越到后面子数组越短, 速度越快.
//* 挖坑法的优点:
// 大部分快速排序算法会同时移动左右两边的指针, 然后交互左右元素. 但由于同时移动了2个指针, 移动到中间的时候很难掌握.
// 挖坑法每次只移动左边或者右边的指针, 然后就开始移动元素(不是交换). 每次只需要考虑一个指针, 且最终2个指针重合, 很容易掌握.
public static void QuickSort<T>(IList<T> list, int left, int right) where T : IComparable<T> //使用 IComparable<T> 而不是 IComparable, 可以节省装箱拆箱的过程. 大幅提高性能.
{
do
{
{
//Swap(s[l], s[(l + r) / 2]); //将中间的这个数和第一个数交换 , 可以防止在集合已经是有序的时候退化到 n*n的复杂度
var temp = list[left];
list[left] = list[(left + right) / 2];
list[(left + right) / 2] = temp;
}
int i = left;
int j = right;
var x = list[i];//取走第一个元素, 作为轴. 在 i 处留下一个坑.
do
{
//左右i,j处的元素和x比较的时候, 都不用等于号, 优点是不会在大部分元的都等于x的时候退化算法的效率.
//比如全部都相同的时候, j直接移动到了最左边. 那么一次调用才排序了第一个元素而已. len长的数组中, 还有len-1的右侧部分需要排序.
while (i < j && list[j].CompareTo(x) > 0)//从最右边开始向左找<=x的元素.
{
j--;
}
if (i < j)
{
list[i] = list[j];//将右边发现的 <= x的元素移动到刚才左边取走元素的坑里(i处). 在 j 处留下一个坑.
i++;//i坑已经被填上了. 将i向右移动.
}
while (i < j && list[i].CompareTo(x) < 0)//从最左边开始向右边找>=x的元素
{
i++;
}
if (i < j)
{
list[j] = list[i];//将左边发现的 >= x的元素移动到刚才右边取走元素的坑里(j处). 在 i 处留下一个坑.
j--;//j坑已经被填上了. 将j向左移动.
}
} while (i < j);
// 循环结束的时候, i和j必须相等.
//Debug.Assert(i == j, $"i==j false. i={i} j={j}");
list[i] = x;//将x填回最后取走元素的坑. 至此. i左边的位置都是<=x的元素, i右边都是>=x的元素. i处是等于x的元素. 这时i处的元素是该元素最终所处的位置了, 后续子排序不用再处理此元素了.
//用循环排序长的那一段, 用递归排序短的那一段.
if (right - i < i - left)
{
if (right > i)//只有一个元素的时候就没必要排序了.
QuickSort(list, i + 1, right);
right = i - 1;//对于较长的那一段 ,这里用循环代替递归. 节省了堆栈所用的空间, 并且防止了在极端情况下的堆栈溢出.
}
else
{
if (i > left)
QuickSort(list, left, i - 1);
left = i + 1;
}
} while (left < right);
}